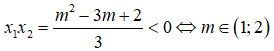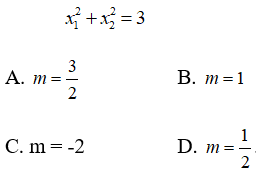
Câu 1: Tìm m để y = x3 – 3x2 +mx – 1 có hai điểm cực trị tại x1, x2 thỏa mãn
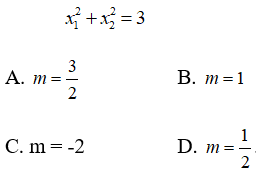
Câu 2: Tìm m để hàm số y = (1/3)x3 – x2 – mx + 1 luôn đồng biến trên từng khoảng xác định của nó
A. m < – 1 B. m > -1 C. m ≤ -1 D. m > -1
Câu 3: Tìm m để phương trình |x3 + 3x2 – 9x + 2| = m có 6 nghiệm phân biệt
A. 0 < m < 3 B. m = 3 C. 3 < m < 29 D. m > -3
Câu 4: Tìm m để hàm số y = -x3 + (2m + 1)x2 – (m2 – 3m +2)x – 4 có cực đại, cực tiểu nằm về hai phía so với trục tung
A. m ∈ (1; 2) B. m ∈ [1; 2]
C. m ∈ (- ∞; 1) ∪ (2; +∞) D. m ∈ (- ∞; 1] ∪ [2; +∞)
Câu 5: Tìm m để hàm số y = x3 – 3mx2 + 12x – 2 nghịch biến trên khoảng (1; 4)
A. m ≥ 5/2 B. m ≤ 5/2 C. m ≤ 2 D. m > 2
Câu 6: Đồ thị hàm số
![]()
có đường tiệm cận ngang có phương trình là
A. y = 1 B. y = 0 C. y = 1/2 D. y = ±1/2
Hướng dẫn giải và Đáp án
| 1-A | 2-C | 3-A | 4-A | 5-A | 6-D |
Câu 1:
y’ = 3x2 – 6x + m.
Hàm số có cực trị khi y’ = 0 có hai nghiệm phân biệt :
9 – 3m > <=> m < 3
Khi đó: x1 + x2 = 2; x1x2 = m/3
![]()
Câu 2:
y’ = x2 – 2x – m ≥ 0, ∀x <=> 1 + m ≤ 0 <=> m ≥ -1
Câu 3:
Vẽ đồ thị y = |x3 + 3x2 – 9x + 2|. Dựa vào đồ thị ta có đáp án A.
Câu 4:
y = -3x2 + 2(2m + 1)x – m2 + 3m – 2 = 0 có hai nghiệm phân biệt.