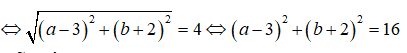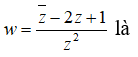
Câu 8: Cho số phức z thỏa mãn: i.z− + z = 2 + 2i và z.z− = 2. Khi đó z2 bằng:
A. 2 B. 4 C. – 2i D. 2i.
Câu 9: Cho số phức z thỏa mãn (1 + i)(z – i) + 2z = 2i. Môđun của số phức:
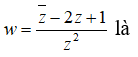
A. 2 B. 4 C. √10 D. 10
Câu 10: Cho số phức z thỏa mãn
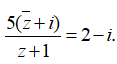
Khi đó môđun của số phức w = 1 + z + z2 là
A. 5 B. √13 C. 13 D. √5
Câu 11: Phương trình z2 – 2z + 3 = 0 có các nghiệm là
A. 2±2√2i B. -2±2√2i C. -1±2√2i D. 1±2√2i
Câu 12: Phương trình z4 – 2z2 – 3 = 0 có 4 nghiệm phức z1, z2, z3, z4. Giá trị biểu thức T = |z1|2 + |z2|2 + |z3|2 + |z4|2bằng
A. 4 B. 8 C. 2√3 D. 2 + 2√3
Câu 13: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z – 2i| = 4 là
A. Đường tròn tâm I(1; -2) bán kính R = 4
B. Đường tròn tâm I(1; 2) bán kính R = 4
C. Đường tròn tâm I(0; 2) bán kính R = 4
D. Đường tròn tâm I(0; -2) bán kính R = 4
Câu 14: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z− + 3 – 2i| = 4 là
A. Đường tròn tâm I(3; 2) bán kính R = 4
B. Đường tròn tâm I(3; -2) bán kính R = 4
C. Đường tròn tâm I(-3; 2) bán kính R = 4
D. Đường tròn tâm I(-3; -2) bán kính R = 4
Hướng dẫn giải và Đáp án
| 8-D | 9-C | 10-B | 11-D | 12-B | 13-C | 14-D |
Câu 8:
Đặt z = a + bi(a, b ∈ R). Ta có: z− = a – bi và z.z− = a2 + b2 = 2(1)
Ta có: i.z− + z = 2 + 2i <=> i(a – bi) + a + bi = 2 + 2i
<=> a + b + (a + b)i = 2 + 2i <=> a + b = 2 (2)
Từ (1) và (2) suy ra a = b = 1. Suy ra z=1+i
Vậy z2 = (1 + i)2 = 1 + 2i – 1 = 2i
Câu 9:
Đặt z = a + bi(a, b ∈ R). Ta có :
(1 + i)(z – i) = (1 + i)[a + (b – 1)i] = a – b + 1 + (a + b – 1)i
Từ giả thiết ta có: (1 + i)(z – 1) + 2z = 2i
<=> a – b + 1 + (a + b – 1)i + 2(a + bi) = 2i <=> (3a – b + 1) + (a + 3b – 1)i = 2i
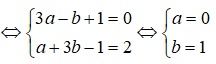
Suy ra z = 1 và
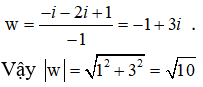
Câu 10:
Đặt z = a + bi(a, b ∈ R). Ta có
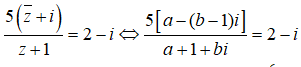
<=> 5a – 5(b – 1)i = (2 – i)(a + 1 + bi)
<=> 3a – b – 2 + (a – 7b + 6)i = 0
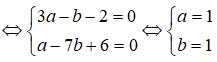
Suy ra z = 1 + i và w = 1 + (1 + i) + (1 + i)2 = 2 + 3i.
Vậy: |w| = √(4 + 9) = √13
Câu 11:
Ta có: Δ’ = 12 – 3 = -2 = 2i2. Phương trình có hai nghiệm: z1,2 = 1 ± 2i
Câu 12:
Phương trình tương đương với: z2 = -1 = i2 hoặc z2 = 3. Các nghiệm của phương trình là: z1 = i, z2 = -i, z3 = √3, z4 = -√-3.
Vậy T = 1 + 1 + 3 + 3 = 8
Câu 13:
Đặt z = a + bi(a, b ∈ R). Ta có:
|z – 2i| = 4 <=> |a + (b – 2)i| = 4
![]()
Vậy tập các điểm biểu diễn số phức z là đường tròn tâm I(0 ;2), bán kính R = 4
Câu 14:
Đặt z = a + bi(a, b ∈ R). Ta có: |z− + 3 – 2i| = 4 <=> |a – bi + 3 – 2i| = 4
<=> |(a + 3) – (b + 2)i| = 4