Câu 1: Cho hai số phức z1 = 2 + 3i, z2 = 1 – 2i . Tìm khẳng định sai
A. z1 + z2 = 3 + i B. z1 – z2 = 1 + 5i
C. z1.z2 = 8 – i D.z1. z2 = 8 + i
Câu 2: Cho hai số phức z1= – 3 + 4i, z2 = 4 – 3i . Môđun của số phức z = z1 + z2 + z1. z2 là
A. 27 B. √27 C. √677 D. 677.
Câu 3: Tìm các số thực x, y sao cho: (1 – 2i)x + (1 + 2i)y = 1 + i
Câu 4: Phần thực và phần ảo của số phức z = (3 + 4i)(4 – 3i) + (2 – i)(3 + 2i) là
A. 32 và 8i B.32 và 8 C. 18 và -14 D. 32 và -8
Câu 5: Cho các số phức z1 = -1 + i, z2 = 1 – 2i, z3 = 1 + 2i . Giá trị của biểu thức T = |z1z2 + z2z3 + z3z1| là
B. 1 B. √13 C. 5 D. 13.
Câu 6:
Hướng dẫn giải và Đáp án
| 1-D | 2-C | 3-A | 4-B | 5-B |
Câu 1:
Tổng của z1 và z2 là z1 + z2 = (2 + 1) + (3 – 2)i = 3 + i
Hiệu của z1 và z2 là z1 – z2 = (2 – 1) + (3 + 2)i = 1 + 5i
Tích của z1 và z2 là z1. z2 = (2 + 3i)(1 – 2i) = 2 – 4i + 3i – 6i2 = 2 – i + 6 = 8 – i
Vậy chọn đáp án D.
Câu 2:
Ta có
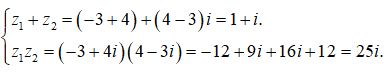
Do đó z = z1 + z2 + z1. z2 = 1 + i + 25i = 1 + 26i
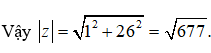
Chọn đáp án C.
Câu 3:
Ta có
(1 – 2i)x + (1 + 2i)y = 1 + i <=> (x + y) + (2y – 2x)i = 1 + i
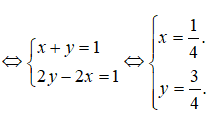
Chọn đáp án A.
Câu 4:
Ta có
z = (12 – 9i + 16i – 12i2) + (6 + 4i – 3i – 2i2) = (12 + 7i + 12) + (6 + i + 2) = 32 + 8i
Chọn đáp án B.
Câu 5:
Ta có:
z2z3 = (1 – 2i)(1 + 2i) = 1 – 4i2 = 5
z1z2 + z1z3 = z1(z2 + z3) = (-1 + i)(1 – 2i + 1 + 2i) = -2 + 2i
Suy ra
![]()
Chọn đáp án B.