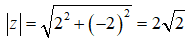
Câu 1: Cho số phức z = 2 – 2i. Tìm khẳng định sai.
A. Phần thực của z là: 2.
B. Phần ảo của z là: -2.
C. Số phức liên hợp của z là z− = -2 + 2i.
D. Môđun của z là
![]()
Câu 2: Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là
A. -1 và 3 B. -1 và -3 C. 1 và -3 D. -1 và -3i.
Câu 3: Môđun của số phức z thỏa mãn z− = 8 – 6i là
A. 2 B. 10 C. 14 D. 2√7
Câu 4: Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4)I = (2x + y) + 2yi.
A. x = 3, y = 1 B. x = 3, y = -1
C. x = -3, y = -1 D. x = -3, y = 1
Câu 5: Hai số phức z1 = x – 2i, z22 + yi (x, y ∈ R) là liên hợp của nhau khi
A. x = 2, y = -2 B. x = -2, y = -2 C. x = 2, y = 2 D. x = -2, y = 2
Câu 6: Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là
A. Hai điểm B. Hai đường thẳng
C. Đường tròn bán kính R=2 D. Đường tròn bán kính R= √2 .
Hướng dẫn giải và Đáp án
| 1-C | 2-B | 3-B | 4-D | 5-C | 6-D |
Câu 1:
Số phức liên hợp của z là z− = -2 + 2i nên chọn đáp án C.
Câu 2:
Ta có z = -1 + 3i => z− = -1 – 3i
Vậy phần thực và phần ảo của z− là -1 và -3.
Chọn đáp án B.
Câu 3:
Ta có
![]()
Chọn đáp án B.
Câu 4:
Ta có (x – 2y) + (x + y + 4)I = (2x + y) + 2yi.
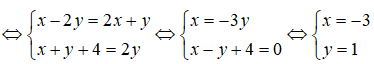
Vậy x = -3, y = 1.
Chọn đáp án D.
Câu 5:
Ta có z1− = x + 2i.
Do đó, hai số phức đã cho gọi là liên hợp của nhau khi và chỉ khi
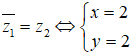
Vậy x= 2, y = 2. Chọn đáp án C.
Câu 6:
Ta có |1 + i| = √(1 + 1) = √2. Gọi M là điểm biểu diễn của z ta có |z| = OM.
Do đó: |z| = |1 + i| <=> OM = √2
Vậy tập hợp các điểm M biểu diễn số phức z là đường tròn tâm O, bán kính R= √2 .
Chọn đáp án D.