
Câu 15: Trong không gian Oxyz, cho hai điểm A(1;3;-2), B(1;1;2). Gọi (P) là mặt phẳng trung trực của đoạn thẳng AB. Phương trình của mặt phẳng (P) là:
A. y – 2z – 2 = 0 B. y – 2z – 7 = 0 C. y – 2z + 3 = 0 D. 2y + z – 4 = 0
Câu 16: Trong không gian Oxyz, cho điểm M(1;-2;3). Gọi M1, M2, M3 lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz. Trong các khẳng định dưới đây, khẳng định nào sai?
A. M1(1; 0; 0)
B. M2(0; 2; 0)
C. M3(0; 0; 3)
D.Phương trình của mặt phẳng (M1M2M3) là:

Câu 17: Trong không gian Oxyz, cho điểm A(2;-3;4). Lập phương trình mặt phẳng (P) đi qua các hình chiếu vuông góc của điểm A trên các trục tọa độ:
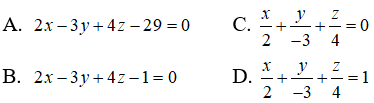
Câu 18: Trong không gian Oxyz, cho điểm M(1;2;3). Lập phương trình mặt phẳng đi qua M sao cho (P) cắt các trục Ox, Oy, Oz lần lượt tại A, B, C và M là trọng tâm của tam giác ABC
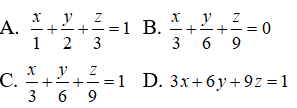
Câu 19: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;-2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC
A. 6x – 3y -2z – 6 = 0
B. x – 2y + 3z + 14 = 0
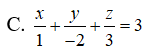
D. x – 2y + 3z – 14 = 0
Câu 20: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(3;2;1) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O) sao cho tam giác ABC đều. Số mặt phẳng (P) thỏa mãn bài toán là:
A. 1 B. 2 C. 3 D. 4
Câu 21: Trong không gian Oxyz, cho mặt phẳng (P) thay đổi nhưng luôn đi qua hai điểm là A(2;0;0), M(1;1;1). Cho (P) cắt các tia Oy, Oz lần lượt tại các điểm B, C (khác O). Viết phương trình mặt phẳng (P) sao cho thể tích của từ diện OABC nhỏ nhất.

Hướng dẫn giải và Đáp án
| 15-A | 16-B | 17-D | 18-C | 19-D | 20-A | 21-B |
Câu 15:
Mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với AB.
Ta có:

Vậy phương trình của mặt phẳng (P) là:
0(x – 1) – 2(y – 2) + 4(z – 0) = 0 <=> y – 2z – 2 = 0
Câu 18:
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c). Vì M(1;2;3) là trọng tâm của tam giác ABC nên ta có:

Vậy phương trình của mặt phẳng (P) là:
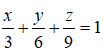
Câu 19:
Ta có: OA → OB, OC => OA → (OBC) => OA → BC
Mặt khác vì AM → BC nên ta suy ra BC → (OAM) => BC → OM
Chứng minh tương tự ta được AC → OM. Do đó OM → (ABC). Ta chọn: np→ = OM→ = (1; -2; 3)
Từ đó suy ra phương trình của mặt phẳng (P) là:
1(x – 1) – 2(y + 2) + 3(z – 3) = 0 <=> x – 2y + 3z – 14 = 0
Câu 20:
Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c > 0 . Phương trình của mặt phẳng (P) là:
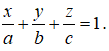
Vì M(3 ;2 ;1) thuộc (P) nên ta có :
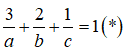
Vì tam giác ABC đều nên ta có :
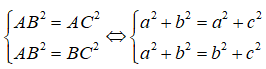
<=> a2 = b2 = c2 <=> a = b= c (do a, b, c > 0)
Thay a=b=c vào phương trình (*) ta được a=b=c=6. Vậy có một mặt phẳng (P) thỏa mãn bài toán.