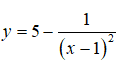
Câu 1: Giá trị lớn nhất của hàm số f(x) = -x2 + 4 là:
A. 0 B. 4 C.2 D. Không có đáp án.
Câu 2: Giá trị lớn nhất của hàm số
đạt được khi x nhận giá trị bằng:
A. 1 B. 5 C. 0 D. Không có đáp án.
Câu 3: Giá trị lớn nhất của hàm số y = x(5 – 2x)2 trên [0; 3] là:
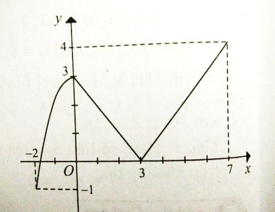
Câu 4: Giá trị lớn nhất của hàm số
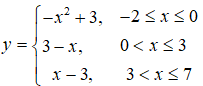
có đồ thị như hình bên là
A. 3 B. 7
B. -1 D. 4
Câu 5: Một công ti quản lí chuẩn bị xây dựng một khu chung cư mới. Họ tính toán nếu tòa nhà có x căn hộ thì chi phí bảo trì của tòa nhà là: C(x) = 4000 – 14x + 0,04x2. Khu đất của họ có thể xây được tòa nhà chứa tối đa 300 căn hộ. Hỏi họ nên xây dựng tòa nhà có bao nhiêu căn hộ để chi phí bảo trì của tòa nhà là nhỏ nhất?
A. 150 B.175 C. 300 D.225
Hướng dẫn giải và Đáp án
| 1-B | 2-D | 3-C | 4-D | 5-B |
Câu 1:
Tập xác định: D = R. Ta có
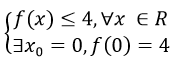
Do đó giá trị lớn nhất của hàm số f(x) là 4 đạt được khi x = 0. Chọn đáp án B.
Câu 2:
Tập xác định: D = R \ {1}
Ta có f(x) ≤ 5, ∀ x ∈ D. Tuy nhiên khi
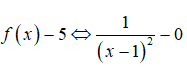
=> không tồn tại x thỏa mãn. Do đó hàm số không có giá trị lớn nhất. Chọn đáp án D.
Câu 3:
y’ = (5 – 2x)(5 – 6x) => y’ = 0
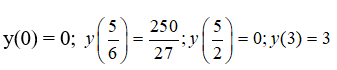
Vậy GTLN của hàm số trên [0; 3] là 250/27 đạt được khi x = 5/6. Chọn đáp án C.
Câu 4:
Chọn đáp án D.
Chú ý. Cần phân biệt giá trị lớn nhất của hàm số và cực đại của hàm số.
Câu 5:
Ta có x là số căn hộ. Rõ ràng x phải thỏa mãn điều kiện 0 ≤ x ≤ 300. Chi phí bảo trì tòa nhà C(x) = 4000 – 14x + 0,04x2
Ta phải tìm 0 ≤ xo ≤ 300 sao cho C(xo) có giá trị nhỏ nhất.
Ta có C'(x) = -14 + 0,08x, 0 ≤ x ≤ 300. C'(x) = 0 <=> x = 175
Trên đoạn [0; 300] ta có C(0) = 4000; C(175) = 2775; C(300) = 3400
Từ đó ta thấy C(x) đạt giá trị nhỏ nhất khi x = 175. Chọn đáp án B.
