Bài 1 (trang 121 SGK Giải tích 12): Tính diện tích hình phẳng giới hạn bởi các đường:
a) y = x2;y = x + 2
b) y =|lnx|;y = 1
c) y = (x-6)2;y = 6x-x2
Lời giải:
a) Giả sử đường thẳng y = x+2 cắt parabol y = x2 tại A và B.
xA, xB là các nghiệm của phương trình:
x2 = x+2 ⇔ x2 – x – 2 = 0
⇔ x = -1; x = 2
Xét hàm f(x) = x2 – x – 2, f’(x) = 2x – 1 = 0 ⇔ x = 1/2

Theo bảng biến thiên ta có: trên đoạn [-1;2] thì x2 – x – 2 < 0
Do đó: |x2 – (x + 2)|= -x2 + x + 2
Vậy diện tích cần tìm là:

b) Hoành độ các giao điểm là:
ln|x|=1 ⇔x=1/e ;x=e
Vậy diện tích cần tìm là:
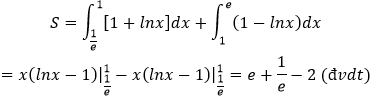
c) Hoành độ giao điểm của hai đồ thị là:
(x-6)2=6x-x2
⇔ (x-6)(2x-6)=0
⇔x=3 ;x=6
Vậy diện tích cần tìm là:
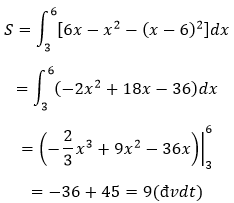
Bài 2 (trang 121 SGK Giải tích 12): Tính diện tích hình phẳng giới hạn bởi đường cong y = x2+1 , tiếp tuyến với đường này tại điểm M(2; 5) và trục Oy.
Lời giải:
Phương trình tiếp tuyến với đường cong y = x2 + 1 tại điểm M(2; 5) là :
y‘=y‘ (2)[x – 2] + 5 ⇔ y = 4x – 3
Điểm M(2; 5) thuộc đường y = x2 + 1 vì 5 = 22 + 1
Vậy diện tích cần tìm là:
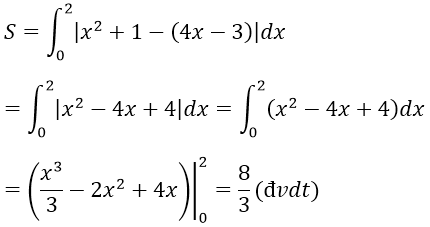
Bài 3 (trang 121 SGK Giải tích 12): Parabol y=x2/2 chia hình tròn có tâm tại gộc toạ độ, bán kính 2√2 thành hai phần. Tìm tỉ số diện tích của chúng.
Lời giải:


Bài 4 (trang 121 SGK Giải tích 12): Tính thể tích khối tròn xoay đó hình phẳng giới hạn bởi các đường sau quay quanh Ox:
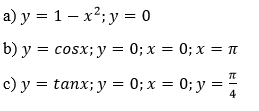
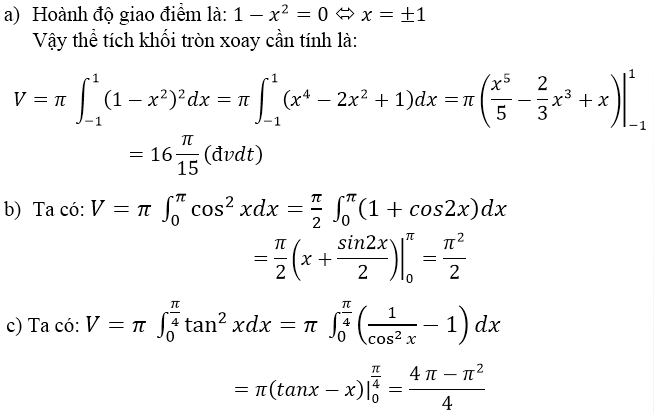
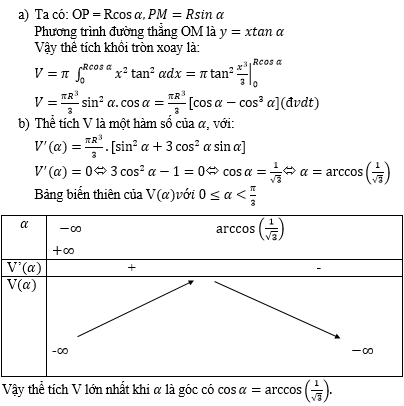
Bài 5 (trang 121 SGK Giải tích 12): Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox.

Lời giải