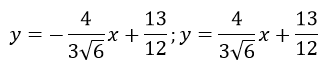Bài 45 (trang 44 sgk Giải Tích 12 nâng cao):
a) Khảo sát và vẽ đồ thị hàm số sau: y=x3-3x2+1
b) Tùy theo các giá trị của m hãy biện luận số nghiệm của Phương trình x3-3x2+m+2=0
Lời giải:
a) TXĐ: R
y’=3x2-6x=3x(x-2)=0
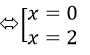
y’> 0 trên khoảng (-∞;0)∪(2; +∞)
y’ < 0 trên khoảng (0; 2)
yCT=y(2)=-3;yCĐ=y(0)=1
![]()
y”=6x-6=6(x-1)=0 <=> x = 1
Bảng xét dấu y’’
| X | -∞ | 0 | +∞ | ||
| Y’’ | – | 0 | + | ||
| Đồ thị | Lồi | điểm uốn u(1; -1) | lõm |
Hàm số lồi trên khoảng (-∞;1)
Hàm số lõm trên khoảng (1; +∞)
Hàm số có 1 điêm uốn u(1; -1)
Bảng biến thiên.
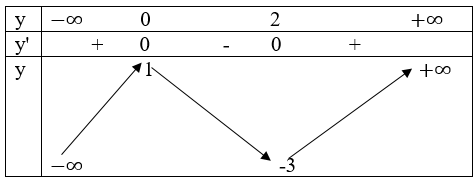
• Đồ thị
Giao với Oy (0; 1)
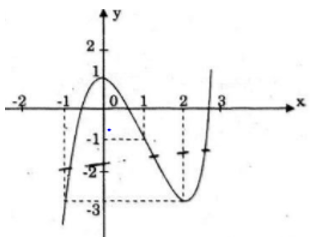
b) x3-3x2+m+2=0 x3-3x2+1=-1-m (2)
Số nghiệm của Phương trình (2) là số giao điểm của đồ thị y=x3-3x2+1 với đường thẳng y = -1 – m.
Dựa vào đồ thị ở câu a) ta có:
– Nếu -1-m > 1<=> m < -2 phương trình (2) có 1 nghiệm.
– Nếu -1-m=1 <=> m = -2: Phương trình (2) có 2 nghiệm.
– Nếu -3 < -1-m < 1 <=> -2 < m < 2: Phương trình (2) có 3 nghiệm
– Nếu -1-m < -3 <=> m > 2: Phương trình (2) có 1 nghiệm
Kết luận:

-2 < m,2. Phương trình (2) có 3 nghiệm
Bài 46 (trang 44 sgk Giải Tích 12 12 nâng cao):
Cho hàm số y=(x+1)(x2+2mx+m+2)
a) Tìm các giá trị của m để đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt.
b) Khảo sát và vẽ đồ thị hàm số với m = -1
Lời giải:
a) Hoành độ giao điểm của đồ thị hàm số (Cm) với trục hoành là nghiệm của phương trình:
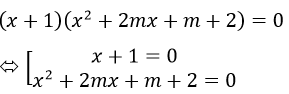
Đặt f(x) = x2+2mx+m+2
Để đồ thị hàm só (Cm ) cắt trục hoành tại 3 điểm phân biệt thì phương trình f(x) = 0 phải có 2 nghiệm phân biệt x1,x2 khác -1.
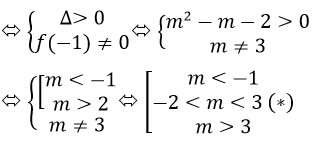
Vậy với m thõa mãn (*) thì đồ thị hàm số Cm cắt trục hoành tại 3 điểm phân biệt.
b) Với m = -1. Ta có: y=(x+1)(x2-2x+1)=x3-x2-x+1
TXĐ: R

Bảng xét dấu y’’
| X | -∞ | 0 | +∞ | ||
| Y’’ | – | 0 | + | ||
| Đồ thị | Lồi | điểm uốn u(1/3;16/27) | lõm |
Hàm số lồi trên khoảng (-∞;1/3)
Hàm số lõm trên khoảng (1/3; +∞)
Hàm số có 1 điểm uốn (1/3;16/27)
Bảng biến thiên
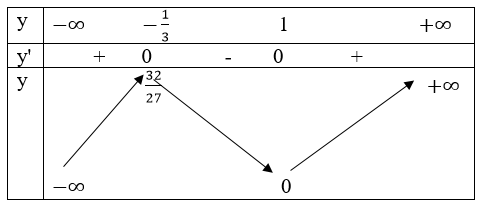
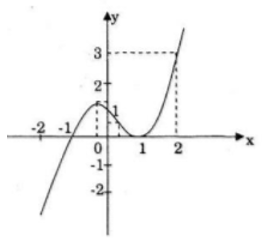
• Đồ thị
Giao với Ox(-1; 0); (1; 0) giao với Oy (0; 1) đi qua (2; 3)
Bài 47 (trang 45 sgk Giải Tích 12 12 nâng cao):
Cho hàm số y=x4-(m+1) x2+m
a) Khảo sát và vẽ đồ thị hàm số với m = 2.
b) CMR đồ thị hàm số đã cho luôn đi qua hai điểm cố định với mọi giá trị của m.
Lời giải:
a) Với m = 2 ta có: y=x4-3x2+2
TXĐ: R
y’=4x3-6x=0 <=> 4x(2x3-3 )=0
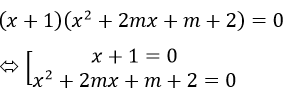
Bảng xét dấu y’’

Bảng biên thiên
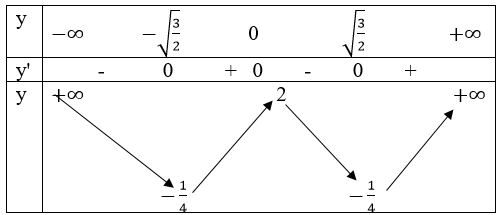
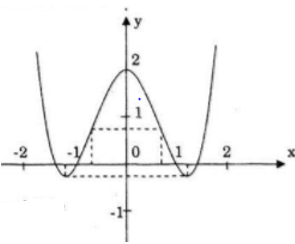
Đồ thị đi qua (1; 0); (-1; 0) (-√2;0),(√2;0),(0;2)
b) Giả sử điểm M(x0;y0) là điểm cố định mà đồ thị hàm số đã cho luôn di qua với mọi m.
Ta có:

Vậy hàm số đã cho luôn đi qua 2 điểm cố định: M1 (-1;0);M2 (1;0)
Bài 48 (trang 45 sgk Giải Tích 12 nâng cao):
Cho hàm số y=x4-2mx2+2m
a) Tìm các giá trị của m sao cho hàm số có 3 cực trị.
b) Khảo sát và vẽ đồ thị của hàm số với m=1/2. Viết Phương trình tiếp tuyến của đồ thị tại 2 điểm uốn.
Lời giải:
a) Ta có y’=4x3-4mx=4x(x2-m)
Để hàm số đã cho có 3 cực trị thì Phương trình y’=0 có 3 nghiệm phân biệt.
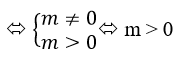
Vậy với m > 0 thì hàm số đã cho có 3 điểm cực trị.
Với m=1/2 ta có y=x4-x2+1
TXĐ: R

Bảng xét dấu y’’

Bảng biến thiên

Đồ thị đi qua (0; 1)
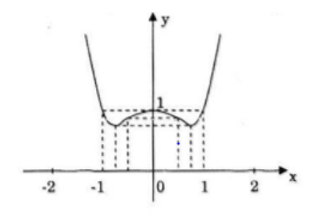
– y=x4-x2+1
Hàm số có 2 điểm uốn là
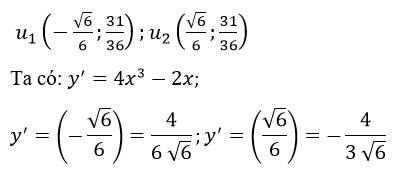
Phương trình tiếp tuyến tại điểm uốn
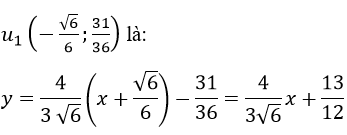
Phương trình tiếp tuyến tại điểm uốn
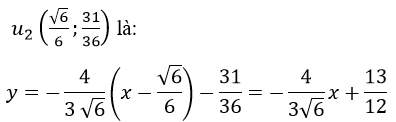
Vậy 2 phương trình tiếp tuyến tại điểm uốn là: