Bài 1 (trang 23-24 SGK Giải tích 12): Tính giá trị lớn nhất và nhỏ nhất của hàm số:
a) y = x3 – 3x2 – 9x + 35 trên các đoạn [-4; 4] và [0; 5]
b) y= x4 – 3x2 + 2 trên các đoạn [0; 3] và [2; 5]

Lời giải:
a) TXĐ: D = R.
y’ = 3x2 – 6x – 9; y’ = 0 => x = –1 hoặc x = 3.
– Xét hàm số trên đoạn [-4; 4]
Vì -1 và 3 đều thuộc đoạn [-4; 4] nên ta tính các giá trị của hàm tại các điểm -4; 4; -1; 3.
Ta có: y(-4) = -41; y(4)= 15; y(-1) = 40; y(3)= 8
Vậy, giá trị lớn nhất của hàm số trên [-4; 4] là:

Giá trị nhỏ nhất của hàm số trên [-4; 4] là:
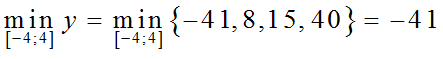
– Trên đoạn [0; 5]: ta thấy y’ = 0 tại x = 3 ∈ [0; 5]
Ta có: y(0) = 35; y(5)= 40; y(3)= 8
Vậy, giá trị nhỏ nhất của hàm số trên [0; 5] là:
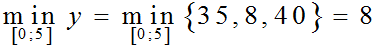
Giá trị lớn nhất của hàm số trên [0; 5] là:
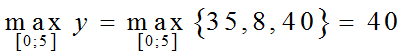
(Các phần b, c, d) dưới đây trình bày theo một cách khác, ngắn gọn hơn, nhưng vẫn bám sát theo cấu trúc trên.
b) TXĐ: D = R
y’ = 4x3 – 6x
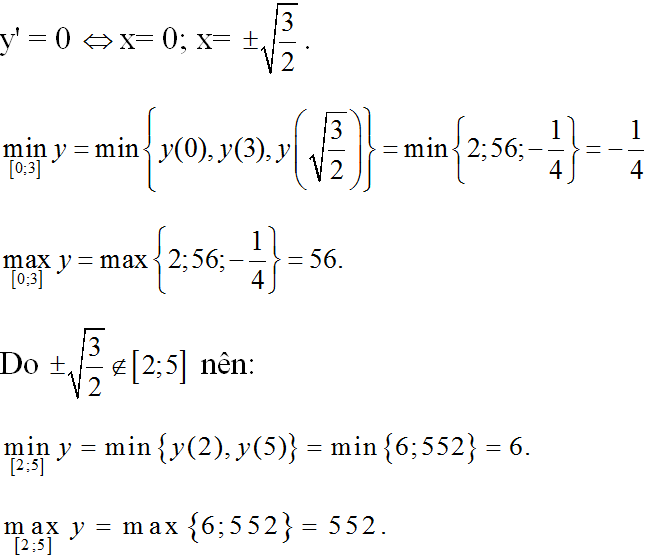
c) TXĐ: D = (-∞; 1) ∪ (1; +∞)
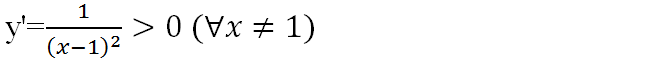
=> Hàm số đồng biến trên D.
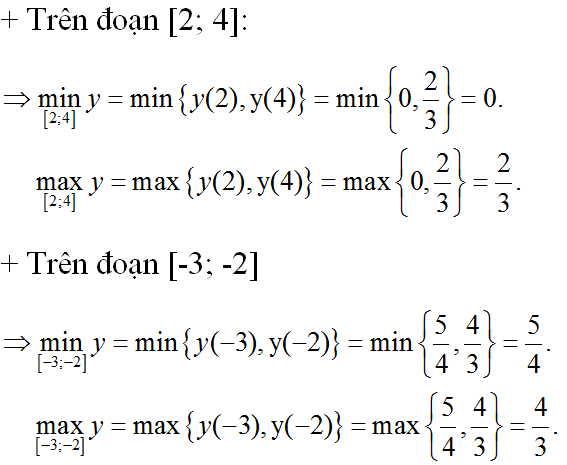
d) TXĐ: D = (-∞; 5/4]
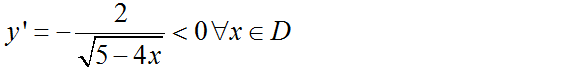
=> Hàm số nghịch biến trên D.
Khi đó trên đoạn [-1; 1]:
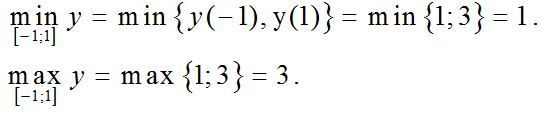
Bài 2 (trang 24 SGK Giải tích 12): Trong số các hình chữ nhật có cùng chu vi 16cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Lời giải:
Nửa chu vi hình chữ nhật là: 16:2 = 8cm
Gọi chiều dài hình chữ nhật là x (cm) thì cạnh kia có độ dài là (8 – x) (cm) (với x ∈ [0; 8]).
Diện tích của hình chữ nhật là:
y = S(x) = x(8 – x) = -x2 + 8x
Xét hàm số trên ta có: D = [0; 8]
y’= -2x + 8 = -2(x – 4)
y’ = 0 => x = 4
![]()
Hàm số đạt giá trị cực đại tại x = 4 (=> cạnh còn lại là 8 – 4 = 4) hay trong số các hình chữ nhật có chu vi 16cm thì hình vuông có diện tích lớn nhất.
(Lưu ý: Thay vì xét max, min như trên, bạn cũng có thể sử dụng Bất đẳng thức Cô-si với hai số x và x – 8 để suy ra kết quả tương tự.)
Bài 3 (trang 24 SGK Giải tích 12): Trong tất cả các hình chữ nhật có diện tích 48 m2, hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Lời giải:
Gọi độ dài một cạnh của hình chữ nhật là x (m) thì độ dài cạnh còn lại là 48/x (m) (điều kiện: x > 0).
Khi đó chu vi hình chữ nhật là:
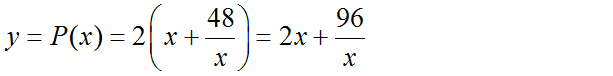
Xét hàm số trên (0; +∞):

Bảng biến thiên:
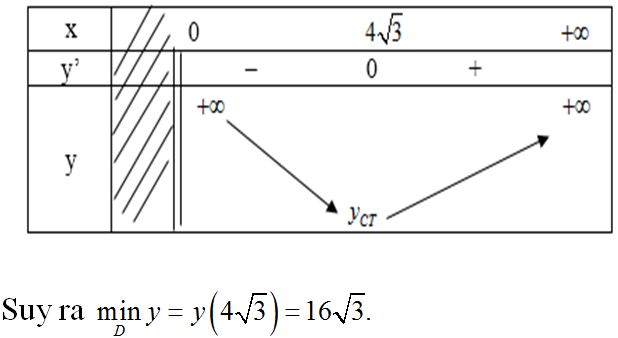
Hàm số đạt cực tiểu tại x = 4√3 hay trong các hình chữ nhật có cùng diện tích 48 m2 thì hình vuông cạnh 4√3 m là hình có chu vi nhỏ nhất.
Bài 4 (trang 24 SGK Giải tích 12): Tính giá trị lớn nhất của các hàm số sau:
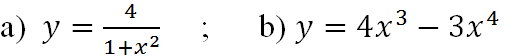
Lời giải:
a) D = R
Ta thấy: 1 + x2 ≥ 1
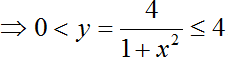
=> Hàm số có giá trị lớn nhất là 4 khi 1 + x2 = 1 => x = 0
Vậy:
![]()
(Cách khác: tính đạo hàm và lập bảng biến thiên)
b) D = R
y’ = 12x2 – 12x3 = 12x2(x – 1)
y’ = 0 => x = 0 ; x = 1
Bảng biến thiên:
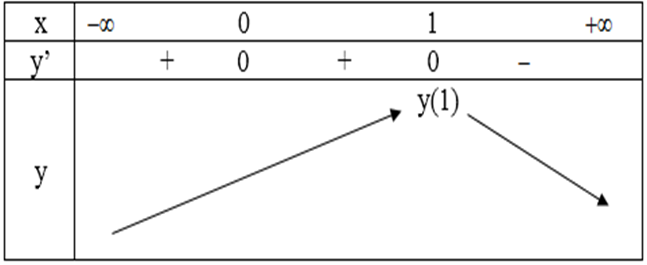
Từ bảng biến thiên suy ra: max y = y(1) = 1
![]()
Bài 5 (trang 24 SGK Giải tích 12): Tính giá trị nhỏ nhất của các hàm số sau:
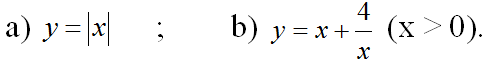
Lời giải:
a)
– Cách 1:
Ta có: y = |x| ≥ 0 ∀ x
=> Hàm số có giá trị nhỏ nhất là min y = 0 khi x = 0.
– Cách 2:
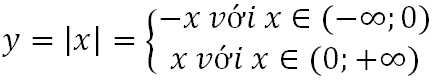
Bảng biến thiên:
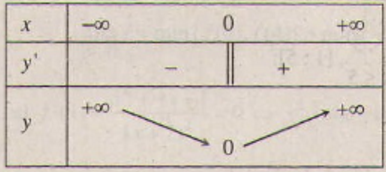
Từ bảng biến thiên suy ra: min y = 0
b) D = (0; +∞)
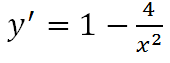
y’ = 0 => x = 2 (loại x = -2 vì ∉ (0; +∞))
Bảng biến thiên:
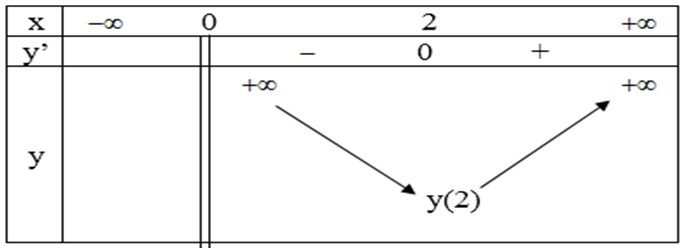
Từ bảng biến thiên suy ra: min y = y(2) = 4



[…] 12 Chương 1 Bài 3 Giá trị lớn nhất và nhỏ nhất của hàm số sẽ giúp các lop12.edu.vn Giải tích – Chương 1 – Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm […]