Bài 1 (trang 9 SGK Giải tích 12): Xét sự đồng biến, nghịch biến của hàm số:
a) y = 4 + 3x – x2
![]()
c) y = x4 – 2×2 + 3
d) y = -x3 + x2 – 5
Lời giải:
(Lưu ý:
Để xét xem dấu của hàm số là + hay – trong một khoảng nào đó ở bảng biến thiên, bạn lấy một giá trị bất kì nằm trong khoảng đó, thay vào đạo hàm y’. Nếu y’ là dương thì dấu của y’ trong khoảng đó là + và ngược lại.
Ví dụ: xét dấu y’ = -x2 + 4 trong khoảng (-2; 2). Chẳng hạn ta lấy một giá trị bất kì trong khoảng là 1, thay vào y’ ta được: y’ = -(-1)2 + 4 = 3 > 0. Do đó dấu của y’ trong khoảng (-2; 2) sẽ là +.)
a) D = R
y’ = 3 – 2x = 0 ⇔ x = 3/2
Bảng biến thiên:
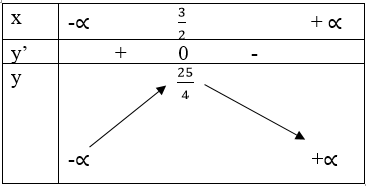
Vậy hàm số đồng biến trong khoảng (-∞; 3/2 ) và nghịch biến trong khoảng ( 3/2 ; + ∞ ).
b) D = R
y’ = x2 + 6x – 7
y’ = 0 ⇔ x = -7 hoặc x = 1
Bảng biến thiên:
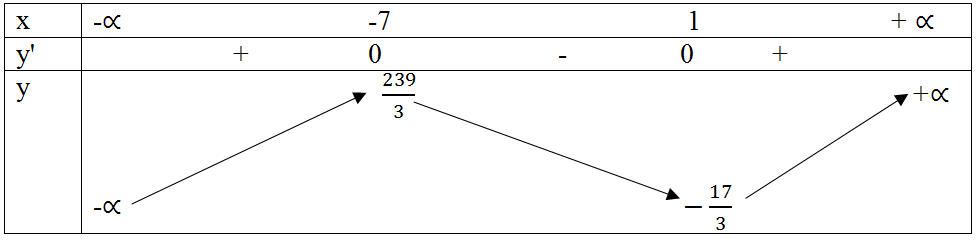
Vậy hàm số đồng biến trong các khoảng (-∞ ; -7) và (1 ; +∞ ); nghịch biến trong khoảng (-7; 1 ).
c) D = R
y’= 4x3 – 4x = 4x(x2 – 1)
y’ = 0 ⇔ x = 0 hoặc x = 1 hoặc x = -1
Bảng biến thiên:
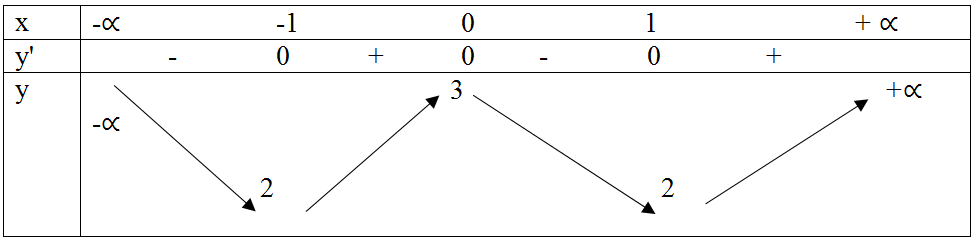
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 1) và (0 ; 1); đồng biến trong các khoảng (-1 ; 0) và ( 1; +∞).
d) D = R
y’= -3x2 + 2x
y’ = 0 ⇔ x = 0 hoặc x = 2/3
Bảng biến thiên:
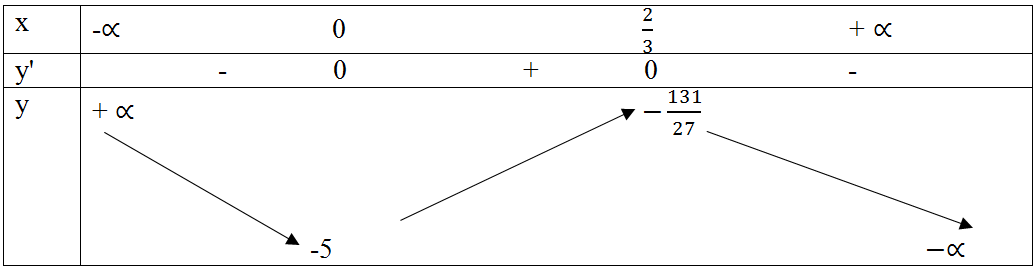
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 0) và (2/3 ; + ∞), đồng biến trong khoảng (0 ; 2/3 ).
Bài 2 (trang 10 SGK Giải tích 12): Tìm các khoảng đơn điệu của các hàm số:
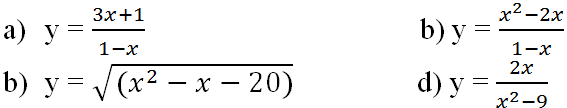
Lời giải:
a) D = R \ {1}
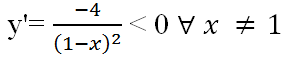
y’ không xác định tại x = 1
Bảng biến thiên:
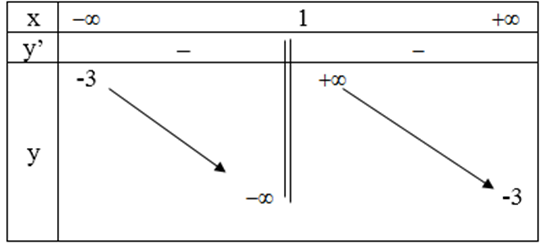
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 1) và (1 ; +∞ ) .
b) D = R \ {1}
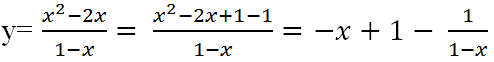
y’ không xác định tại x = 1
Bảng biến thiên:
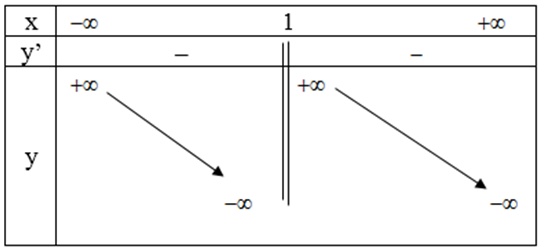
Vậy hàm số nghịch biến trong các khoảng (-∞ ;1) và (1 ; +∞)
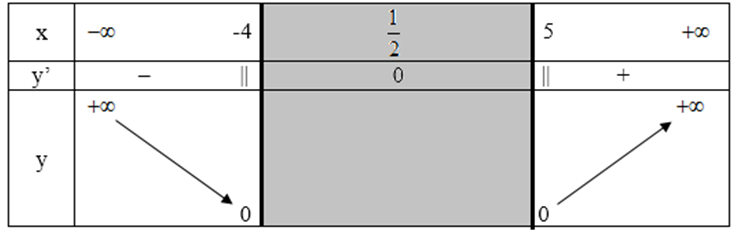
c) D = (-∞ ; -4] ∪ [5; +∞)
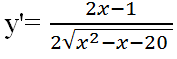
y’ không xác định tại x = -4 và x = 5
Bảng biến thiên:
Vậy hàm số nghịch biến trong nửa khoảng (-∞ ; -4] và đồng biến trong nửa khoảng [5 ; + ∞ ).
d) D = R \ {±3}
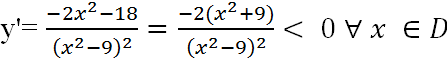
y’ không xác định tại x = ±3
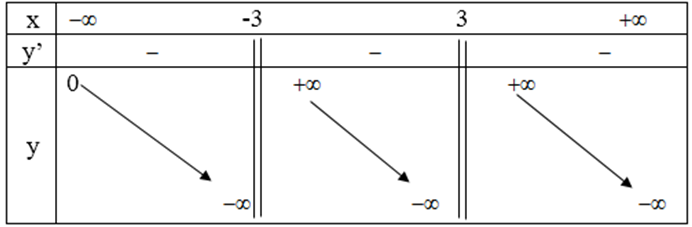
Bảng biến thiên:

Vậy hàm số nghịch biến trong các khoảng đó nên hàm số nghịch biến trong khoảng (-∞ ; -3) ( -3; 3) và (3; +∞ )
Bài 3 (trang 10 SGK Giải tích 12): Chứng minh rằng hàm số
![]()
đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).
Lời giải:
TXĐ: D = R
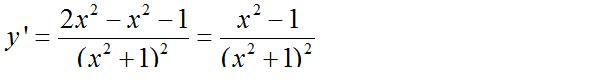
y’ = 0 => x = ±1
Bảng biến thiên:
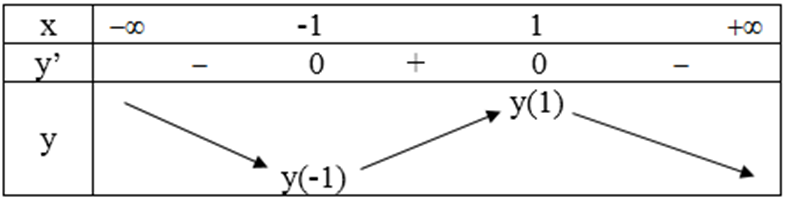
Vậy hàm số đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞) (đpcm).
Bài 4 (trang 10 SGK Giải tích 12): Chứng minh rằng hàm số
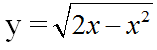
đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Lời giải:
TXĐ: D = [0; 2]
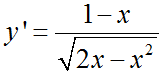
y’ = 0 => x = 1
Bảng xét dấu y’:

Từ bảng trên ta có:
+ y’ > 0 với x ∈ (0; 1) do đó đồng biến trên khoản (0; 1);
+ y’ < 0 với x ∈ (1; 2) nên nghịch biến trên khoảng (1; 2).
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2) (đpcm).
Bài 5 (trang 10 SGK Giải tích 12): Chứng minh các bất đẳng thức sau:
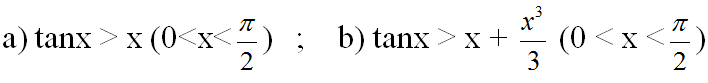
Lời giải:
a) Xét hàm số y= f(x) = tanx – x trên khoảng (0; π/2)
Ta có:
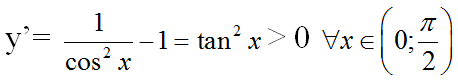
=> hàm số đồng biến trên khoảng (0; π/2)
Do đó với x > 0 => f(x) > f(0) hay tanx – x > 0
=> tanx > x ∀ x ∈ (0; π/2) (đpcm)
b) Xét hàm số
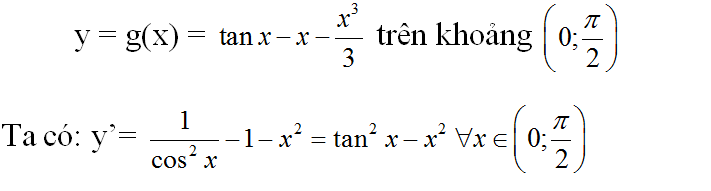
Theo kết quả câu a) thì tanx > x ∀ x ∈ (0; π/2)
Suy ra g'(x) > 0 ∀ x ∈ (0; π/2)
=> hàm số g'(x) đồng biến trên khoảng (0; π/2)
Do đó với x > 0 => g(x) > g(0)
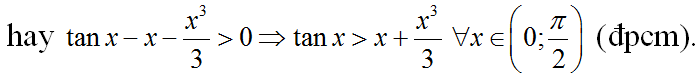


[…] toán xét tính đồng biến, nghịch biến của hàm số trên tập số thực R… lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] khoảng nào sau đây ?(0; +)(-)32;+∞3(-x;0). giasuthanhtai.com.vn giasuthanhtai.com.vn lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] biến … sachbaitap.com Bài 1. Sự đồng biến, nghịch biến của hàm số lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] biến, nghịch biến của hàm số – Tìm đáp án, giải bài tập, để học tốt lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] hoc360.net bám sát với nội dung sách giáo khoa và chương trình của bộ giáo … lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] đơn điệu của các hàm số: a) y = 14{x^4} – 2{x^2} – 1 (đbtrên (-2; 0), (2; +), lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] vận dụng vi.wikipedia.org Thành viên:Chichbongtrando25 – Wikipedia tiếng Việt lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] học ở lớp 9, lớp 10 và lớp 12. Định nghĩa hàm số đồng biến, hàm số… lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] trá»±c tuyến hà ng Äầu Viá»t Nam hoctoan24h.net hoctoan24h.net lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] trẽn K nếu: VX1, Xỉ e K, X1 f(xi) < f(X2) Hàm số y – f(x) nghịch biến … lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] biến trên khoảng nào? Hàm số (y = 2(x^4) + 1 ) đồng biến trên khoảng nào? lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] xích trực tiếp đến các bài học sau của chương này và một số chương sau. lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] biến trên K nếu Nếu hàm số nghịch biến trên K thì đồ thị của hàm số lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] – Khóa học : Luyện Thi Đại Học Môn Toán Hàm số đồng biến, nghịch biến lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] hàm như sau:Hàm số $y = f({x^2} + 2x)$ đồng biến trên khoảng nào dưới đây? lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] . – Nắm định lí về tính đơn điệu và dấu của đạo hàm . – Vận dụng lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] số chương sau. thuvienhoclieu.com thuvienhoclieu.com hoctoan24h.net hoctoan24h.net lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] trực tuyến hàng đầu Việt Nam * Học mọi lúc, mọi nơi ✅ Hotline 1: 1900099926 lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] khoang tại 123doc – ThÆ° viá»n trá»±c tuyến hà ng Äầu Viá»t Nam lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] tích lớp 12. Bài: Sự đồng biến, nghịch biến của hàm số – Chương 1. Giải lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] Äá»NG BIẾN, NGHá»CH BIẾN môn toán edusmart.vn edusmart.vn lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]
[…] học tập sachbaitap.com Bài 1. Sự đồng biến, nghịch biến của hàm số lop12.edu.vn Giải tích – Chương 1 – Bài 1: Sự đồng biến, nghịch biến của hàm số Bài 1 […]