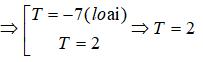Câu 1: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox.
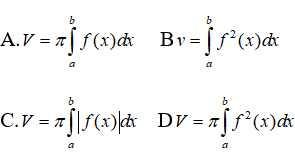
Câu 2: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x3 – x và đồ thị hàm số y = x – x2.
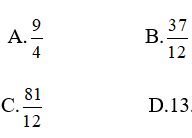
Câu 3: Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = (x -1)e2x ,trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox
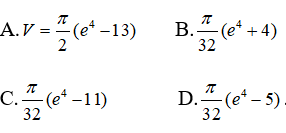
Câu 4: Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người).
a) Có bao nhiêu trẻ được sinh trong khoảng thời gian này ( tức là trong 10 năm đầu tiên sau chiến tranh)?
A. 100 triệu B. 120 triệu C. 150 triệu D. 250 triệu.
b) Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.
A. 1 năm B. 2 năm C. 3 năm D. 4 năm.
Hướng dẫn giải và Đáp án
| 1-D | 2-B | 3-A | 4: a – C; b – B |
Câu 2:
Tìm hoành độ các giao điểm của hai đồ thị, ta có:
x3 – x = x – x3 <=> x3 + x2 – 2x = 0
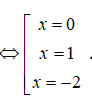
Vậy diện tích của hình phẳng tính là
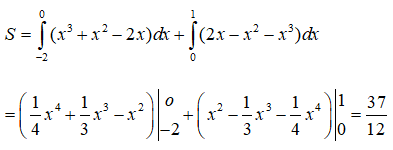
Vậy chọn đáp án B.
Câu 3:
Tìm hoành độ giao điểm của hai dồ thì, ta có:
(x – 1)e2x = 0 => x = 1
Vậy thể tích của khối tròn xoay thu được khi quay (H) quanh Ox được tính bởi
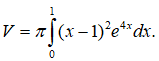
Đặt: u = (x – 1)2, dv e4xdx. Ta có du = 2(x -1)dx và v = e4x/4 .
Áp dụng công thức tích phân từng phần ta được
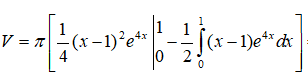
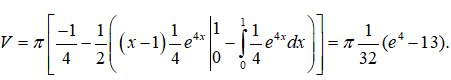
Đặt u1 = x – 1, dv1 = e4xdx , ta có du1 = dx, v1 = e4x/4 .
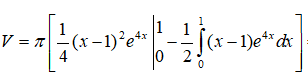
Vậy chọn đáp án A.
Câu 4:
a) Để tìm số trẻ mới sinh, chúng ta sẽ tính tích phân tỉ lệ sinh b(t) trên khoảng thời gian 10 năm đầu tiên sau chiến tranh
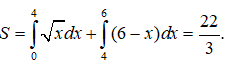
Vậy số trẻ được sinh cần tìm là 150 triệu.
Chọn đáp án C.
b) Số lượng trẻ mới sinh trong khoảng thời T bằng:
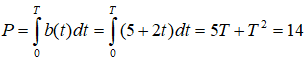
Chọn đáp án B.